物以类聚人以群分

KMeans

简介

k-means应该是最简单的一个聚类算法了，它的优化目标是使所有数据点到它们各自的最近类别中心的距离总和最小。其实k-means是基于质心的聚类，它假设类别的形状是球形的，并通过EM的方法进行求解。它的缺点是对噪声敏感，无法发现任意形状的类别，不稳定。 优化目标：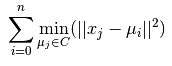

算法过程

1. 首先随机选出k个数据作为类别中心
2. 然后将其他数据分配到距离他们最近的类别中
3. 将类别中心更新为所有这个类别中的数据的均值
4. 迭代2和3，直至算法稳定

k-means++

由于k-means受初始中心的影响严重，而随机选择很可能使得中心分布不均匀。k-means++的想法就是通过控制生成初始中心的过程来使得中心分布均匀，具体为顺序选择初始中心，使得新选择的中心距离已有的中心尽可能地远。初始中心的过程如下：

1. 首先随机选择一个中心
2. 然后计算其他数据点到已有中心的最近距离记为D(x)
3. 按照按照概率从数据点中选取下一个中心，每个数据点被选取的概率＝
   
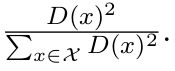
4. 迭代2和3直至选出k个中心

DBSCAN

简介

DBSCAN算法是一种基于密度的聚类算法，它的优势是能够发现任意形状的类别(database2)，而k-means只能发现凸(convex)的形状，同时DBSCAN还有很强的抗噪性(database3)。并且DBSCAN只需扫描一遍数据集即可完成聚类，而不用迭代执行。

相关定义

DBSCAN需要使用两个参数来定义密度：半径阈值Eps以及在这个半径内的邻居个数MinPts。

1. Eps近邻：数据p的Eps近邻指的是那些与其距离小于Eps的数据
   

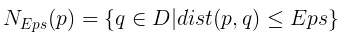
2. 核心数据点：那些Eps近邻数量大于MinPts的数据点

3. 直接密度可达：从q直接密度可达p指的是，p是q的Eps近邻并且q是一个核心数据点
   

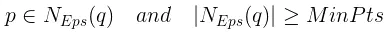
4. 密度可达：从q密度可达p指的是，存在一个数据链p1,p2…pn，其中p1是q，pn是p，并且从pi直接密度可达pi+1

5. 密度相连：p与q密度相连指的是，存在一个数据点o，使得从o可同时密度可达p与q

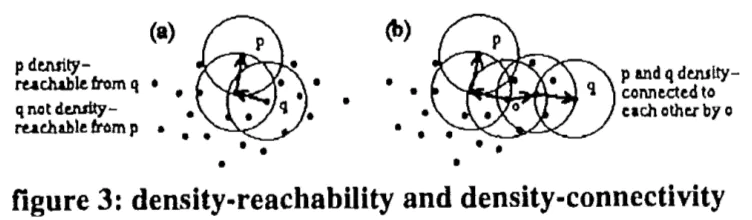
其实，以上这些定义都是为了说明在DBSCAN模型中，究竟一个类别代表什么含义。它定义一个类别中的任意两个点或者是密度可达的或者是密度相连的。可以这样想：每一个数据点都是一个人，而那些核心数据点就是有影响力的人。那么一个人可以通过找到身边的有影响力的朋友来认识新的朋友，如果这个新朋友恰巧也是有影响力的人的话，就又可以通过他再认识一堆新朋友。

算法流程

DBSCAN只需扫描一遍数据库，在扫描的过程中判断当前数据q是否是核心数据点，如果是的话，那么就发现了一个新的类别，并且在添加新的数据点时将它们标记为这个类别，首先将q还没有标记类别或者标记noise的Eps近邻都添加进去，而如果新添加的近邻也是核心数据点的话，就再添加其没有类别或者标记noise的Eps近邻，直至不能再添加新的结点；如果不是的话，就将q标记为noise并跳到下一个数据点。扫描之后，标记为noise的数据点就是噪声数据。

由于SCAN的思想与DBSCAN一致，区别只是计算距离的方法不同，因此没有另外实现。代码参见

其它

时间复杂度

DBSCAN需从数据库中寻找到一个指定数据的Eps近邻，而这需要扫描全部数据库。通过R*-trees可以优化这种区域查找，使得能够log时间完成。所以最终的时间复杂度为O(nlong(n))。

选择参数

[2]中提出一种启发式的方法来选择那个最稀疏类别的参数，首先计算出所有数据点的第k个近邻与它的距离，将其降序排序并绘制二维图。然后选择出第一个抖动大的数据的值即可。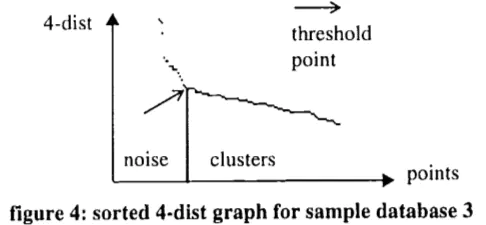

参考文献

1. k-means++: The Advantages of Careful Seeding
2. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise
3. SCAN: A Structural Clustering Algorithm for Networks