社区发现的第一个算法

社区发现

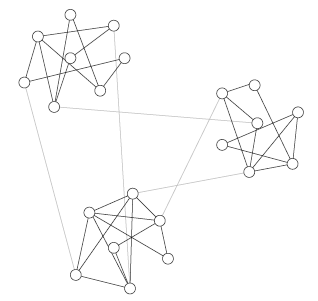
先来说说什么是社区发现吧，学术上的说法是：一个社区由一组连接紧密的结点组成，同时这些结点与社区外部的结点连接稀疏，如下图所示。那么，社区发现就是在复杂网络中发现这些连接紧密的社区结构。其实，我个人觉得，社区发现就是网络中的结点聚类。

GN算法

GN算法[1]是社区发现中的第一个算法，也就是它开启了这个研究领域。它的基本思想是删除掉那些社区之间的连接，那么剩下的每个连通部分就是一个社区。那么问题来了，就是哪些是社区之间的边呢？作者巧妙地借助最短路径解决了这个问题，他们定义一条边的介数(betweeness)为网络中所有结点之间的最短路径中通过这条边的数量，而介数高的边要比介数低的边更可能是社区之间的边。其实，这也比较好理解，因为两个社区中的结点之间的最短路径都要经过那些社区之间的边，所以它们的介数会很高。

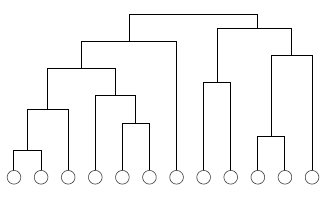
GN算法每次都删除网络中介数最大的边，直至网络中的所有边都被删除。这样GN的过程对应着一颗自顶向下构建的层次树。在层次树中选择一个合适的层次分割即可。

GN算法的准确性很好，但是时间复杂度却太高，显然找到所有最短路径很耗时。使用[2]中的方法计算介数的时间复杂度为O(mn)，所以GN的时间复杂度为O(m2n)，m是边数量，n是结点数量。

代码

import networkx as nx

import sys
sys.path.append('../')

from util.graph_helper import load_graph
from util.graph_helper import clone_graph
from util.modularity import cal_Q

#paper: Community structure in social and biological networks

class GN:
    
    def __init__(self, G):
        self._G_cloned = clone_graph(G)
        self._G = G
        self._partition = [[n for n in G.nodes()]]
        self._max_Q = 0.0
        
    def execute(self):
        while len(self._G.edges()) != 0:
            edge = max(nx.edge_betweenness(self._G).items(),key=lambda item:item[1])[0]
            self._G.remove_edge(edge[0], edge[1])
            components = [list(c) for c in list(nx.connected_components(self._G))]
            if len(components) != len(self._partition):
                cur_Q = cal_Q(components, self._G_cloned)
                if cur_Q > self._max_Q:
                    self._max_Q = cur_Q
                    self._partition = components
        print self._max_Q
        print self._partition
        return self._partition
        
    
if __name__ == '__main__':
    G = load_graph('../network/club.txt')
    algorithm = GN(G)
    algorithm.execute()
    #print len(G.edges(None, False))

参考文献

1. Community structure in social and biological networks
2. Finding and evaluating community structure in networks