Graphx中的三角计数
在网络中计算节点的重要性有着比较多的应用, 比如找到一些大点进行信息传播或者找到一些异常点进行风险判定等。
有几种常用的方法:
- betweeness(界数):首先找到网络中的所有最短路径,然后对每个最短路径中的节点计数,值越大越重要。这种方法找到的是网络中“媒介”或者说“桥接”属性比较强的节点,但是有个关键的问题是时间复杂度太大。
- pagerank:还可以用pagerank计算网络中比较“权威”的点,或者其它的传播类算法应该也是可以的。
这里介绍一种基于三角计数的方法。网络中的三角形指的是三个节点中的任意两个节点都存在边,可以认为是弱化版的“团(Clique)”。如果一个节点能够频繁地和多个不同节点之间形成这种三角形结构,那么这个点的周围一定是比较稠密的,并且这个点也是其中有重要影响力的。以社交网络举例会比较好理解:三个人之间都存在好友关系的话基本可以认为是一个小群,然后一个人又和大量的不同人都在一个小群中的话,那TA一定是个社交达人了。
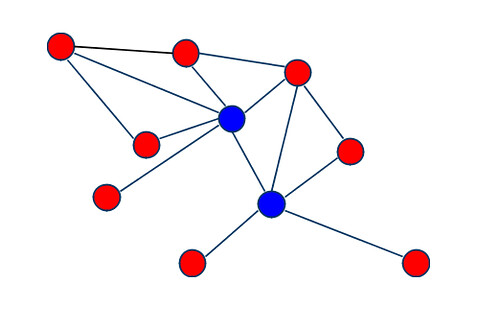
Graphx中已经封装好了现成的算法可以调用,Triangle-Counting的实现思路也很简单。具体来说有以下三步:
- 计算出每个节点的邻居节点集合
- 对于每个边计算出两个节点的交集,并将交集大小传递给两个节点
- 对于每个节点计算接收到的累加值并除以2(这个点在三角形有两条边)
The algorithm is relatively straightforward and can be computed in three steps:
- Compute the set of neighbors for each vertex.
- For each edge compute the intersection of the sets and send the count to both vertices.
- Compute the sum at each vertex and divide by two since each triangle is counted twice.
Spark在执行这个算法之前会对网络进行一些标准化的处理,如果输入已经是标准化的话,那么可以直接调用runPreCanonicalized方法来减少开销
There are two implementations. The default TriangleCount.run implementation first removes self cycles and canonicalizes the graph to ensure that the following conditions hold:
- There are no self edges
- All edges are oriented (src is greater than dst) 确保两个点之间只有一条边
- There are no duplicate edges
However, the canonicalization procedure is costly as it requires repartitioning the graph.
If the input data is already in “canonical form” with self cycles removed then the TriangleCount.runPreCanonicalized should be used instead.
val canonicalGraph = graph.mapEdges(e => 1).removeSelfEdges().canonicalizeEdges()
val counts = TriangleCount.runPreCanonicalized(canonicalGraph).vertices
源代码:
1 | object TriangleCount { |
关于clique的信息可以参考:http://codelibrary.tech/ml/community_cpm.html
评论系统未开启,无法评论!